Understanding Partial Application of Function Composition
A recent post on r/haskell solicited help understanding the expression
isAllergicTo :: Allergen -> Int -> Bool
isAllergicTo = (. allergies) . elemwhere Allergen is a type and allergies :: Int -> [Allergen].
It’s straightforward to rewrite this function pointfully (ie. with formal parameters in place), but doing so doesn’t help one develope an intuition for thinking about function composition, partially applied, on a higher semantic level. This post is my attempt at helping people develop that high-level intuition.
The Problem
The original problem had allergies :: Int -> [Allergen], but I am going to change Int there to PatientId.
I find that this helps to ground the problem.
data PatientId
data Allergen
instance Eq Allergen
allergies :: PatientId -> [Allergen]
allergies = undefined "elided"
isAllergicTo :: Allergen -> PatientId -> Bool
isAllergicTo = (. allergies) . elemOur job is to “git gud” at Haskell to the point that we can glance at the definition of isAllergicTo and intuitively grasp how it works.
I’m not quite there yet, either, so don’t feel bad.
Another thing that I find helps me understand the problem more deeply is to eliminate incidental details.
We can reformulate the essential concepts of the problem, without distracting details, as follows.
We postulate that some types A and B exist along with a function f :: A -> B between them.
We’ll also need B to have a notion of equality between members.
To avoid dragging lists into the problem unnecessarily, I’ll replace elem with (==).
I’ll also define and alias eq = (==) for code readability.
data A
data B
instance Eq B
eq :: B -> B -> Bool
eq = (==)
f :: A -> B
f = undefined "elided"
isEq :: B -> A -> Bool
isEq = (. f) . eqOur goal is to be able to read and understand things like isEq = (. f) . eq when we come across them in code.
Notice that isEq in our stripped-down version of the problem is directly analogous to isAllergicTo from the original version of the problem.
In order to appeal to the broadest number of different areas of your brain, I’ll carry on referring to both the isAllergicTo form of the problem and the isEq form of the problem, in parallel.
Focus on the one that resonates with you the most, or compare and contrast them as we go.
Prologue: Rewriting in Pointful Style
Let’s first make sure that we have a very good understanding of isAllergicTo before we move on.
To do so, we’ll rewrite it with explicit parameters.
We end up with isAllergicTo a p = elem a (allergies p).
A moment’s intuition tells us that this function answers the question, is a one of p’s allergies.
Seeing isAllergicTo in pointful form, its inner workings are immediately clear to me.
Its inner workings were not at all clear to me having seen isAllergicTo in its pointfree form, but we can fix that.
Before we go on, I want to draw your attention back to a step that I find particularly interesting.
\[\begin{align*} &= \left( \mathop\circ \mathtt{allergies} \right) \left( \mathtt{elem} \, a \right) \\ &= \mathtt{elem} \, a \mathop\circ \mathtt{allergies} \\ \end{align*}\]Two things pique my curiosity here.
First, notice how \( \mathtt{elem} \, a \) sits on the right-hand side of \( \left( \mathop\circ \mathtt{allergies} \right) \), so it’s earlier in the computational pipeline. But this step flips it, so that \( \mathtt{elem} \, a \) ends up on the left-hand side of \( \left( \mathop\circ \mathtt{allergies} \right) \), so later in the computational pipeline. It’s as though something is swapped around.
Second, I like the interplay between function composition and function application in this step. Before the step, the function \( \left( \mathop\circ \mathtt{allergies} \right) \) is applied to its argument \( \mathtt{elem} \, a \). After the step, we’re left with the composition of the functions \( \mathtt{allergies} \) and \( \mathtt{elem} \, a\). It’s as though function application on one level becomes function composition at another level.
Put a couple pins in those observations.
For completeness, here’s isEq’s rewrite.
It’s a little bit easier on the eyes, thus a little bit easier to follow, in my opinion.
We’d like to train ourselves to be able to read things like (. f) . eq or (. allergies) . elem naturally.
The process of such training is a bit involved, but we only have to go through the process once.
By the time we’re through, we will have a clear, concise, high-level intuition for what things like (. f) and (. allergies) mean.
Building a Higher Vantage Point
I like thinking in pictures.
We presuppose a function allergies :: PatientId -> [Allergen] (or f :: A -> B, respectively).
That looks like this.
![Figure 1: the function allergies depicted as an arrow from PatientId to [Allergen]](/assets/img/understanding-function-composition/figure-1.png )
Figure 1: the function allergies depicted as an arrow from PatientId to [Allergen]
In Figure 1 and the subsequent figures, we depict types as nodes in a directed graph. Then a function can be visualized as an arrow from its source type to its target type.
Now, consider some arbitrary function \( g \) with source type [Allergen] (respectively, B) and target type \( w \).
Adding a node for \( w \) and an arrow for \( g \) gives us a graph with a path in it.
This graph will also have an implied arrow from PatientId (res. A) to \( w \): specifically, I’m talking about the composition of \( g \) and allergies (res. f).
This composed function can be thought of as the result of following the path from PatientId, along allergies through [Allergen], along \( g \) to \( w \) (res. from A, along f through B, along \( g \) to \( w \)).
![Figure 2: a two-arrow path representing the composition of allergies with a function g from [Allergen] to w](/assets/img/understanding-function-composition/figure-2.png )
Figure 2: a two-arrow path representing the composition of allergies with a function g from [Allergen] to w
Figure 2 has a bonus feature that I haven’t brought up yet. You may have noticed it. It’s \( \mathop{\widehat{\mathtt{allergies}}} g \) (res. \( \mathop{\widehat{\mathtt{f}}} g \)). This is a new operation on functions that I’d like to now define. For any function \( x \), define \( \widehat{x} \) to be the higher-order function that takes a function \( y \) to the composition \( y \mathop\circ x \) (if the composition is defined). That’s quite a mouthful. Let’s try to see it, in symbols; seeing the same thing two ways always helps me. Compare the symbolic description below to the verbal description above and practice translating between the two.
\[\begin{align*} \mathop{\widehat{x}} y &= y \mathop\circ x &\text{if $\mathrm{source}(y) = \mathrm{target}(x)$} \end{align*}\]I’ll call this operation “hat,” and I’ll refer to things like \( \widehat{x} \) as “ex-hat.” As a third way to think of the hat operation, this is what it looks like in code.
hat :: (a -> b) -> ((b -> w) -> (a -> w))
hat f = (. f)Hopefully it’s becoming clear why I would go to the trouble of defining the hat operation. The hat operation exists in order to give a name to the code pattern we’re trying to understand: function composition partially applied.
Look again at the signature of hat.
I could have written (a -> b) -> (b -> w) -> a -> w, since that’s equivalent and omits implied parentheses.
I chose to include all of the implied parentheses when I wrote hat’s signature.
We aim to focus on what we get when we partially-apply function composition.
Equivalently, we now focus on the function returned by hat.
f :: a -> b
hat f :: (b -> w) -> (a -> w)Figure 3 represents that code visually. It depicts the function \( \mathtt{f} \) going from its source type \( \mathtt{A} \) to its target type \( \mathtt{B} \) and the function \( \widehat{\mathtt{f}} \) going from its source type \( \mathtt{B} \to w \) to its source type \( \mathtt{A} \to w \). In the concrete setting, that’s the function \( \mathtt{allergies} \) going from its source type \( \mathtt{PatientId} \) to its target type \( [\mathtt{Allergen}] \) and the function \( \widehat{\mathtt{allergies}} \) going from its source type \( [\mathtt{Allergen}] \to w \) to its target type \( \mathtt{PatientId} \to w \).
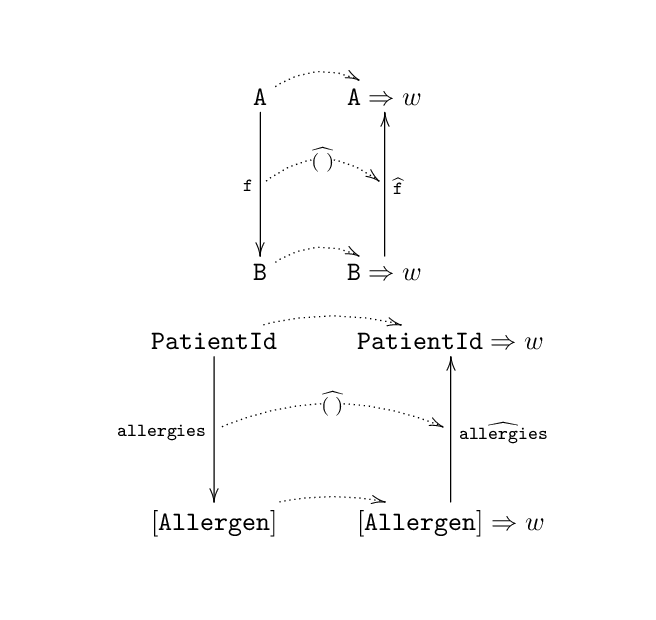
Figure 3: a series of three arrows representing the action of the hat operation on allergies
Here is some intuition we can gain from Figure 3. First, in addition to transforming functions, \( \widehat{(\;)} \) appears to have some kind of action on types, sending a type \( x \) to \( x \to w \). Second, \( \widehat{(\;)} \) seems to reverses the direction of arrows it transforms. We depict this in Figure 4.
![Figure 4: the hat operation transforming functions with source type PatientId and target type [Allergen] into higher-order functions with source type [Allergen] -> w and target type PatientId -> w](/assets/img/understanding-function-composition/figure-4.png )
Figure 4: the hat operation transforming functions with source type PatientId and target type [Allergen] into higher-order functions with source type [Allergen] -> w and target type PatientId -> w
So \( \widehat{(\;)} \) takes a function and returns a higher-order function with reversed arguments, in some sense. That’s a start, but it’s still very vague. We can temper this understanding by zooming in and considering what \( \widehat{\mathtt{allergies}} \) specifically does (res. what \( \widehat{\mathtt{f}} \) does).
As a function, \( \widehat{\mathtt{allergies}} \) has source type \( [\mathtt{Allergen}] \to w \) and target type \( \mathtt{PatientId} \to w \). (Respectively, \( \widehat{\mathtt{f}} \) has source type \( \mathtt{B} \to w \) and target type \( \mathtt{A} \to w \).)
\[\begin{align*} \widehat{\mathtt{f}} &: \left( \mathtt{B} \to w \right) \to \left( \mathtt{A} \to w \right) \\ \widehat{\mathtt{allergies}} &: \left( [\mathtt{Allergen}] \to w \right) \to \left( \mathtt{PatientId} \to w \right) \end{align*}\]Figure 5 depicts the action of \( \widehat{\mathtt{allergies}} \) (res. \( \widehat{\mathtt{f}} \)) on an arbitrary function \( g \). You can think of this as “stretching out” the source and target sets in the signature of \( \widehat{\mathtt{allergies}} \) (res. \( \widehat{\mathtt{f}} \)) given above.
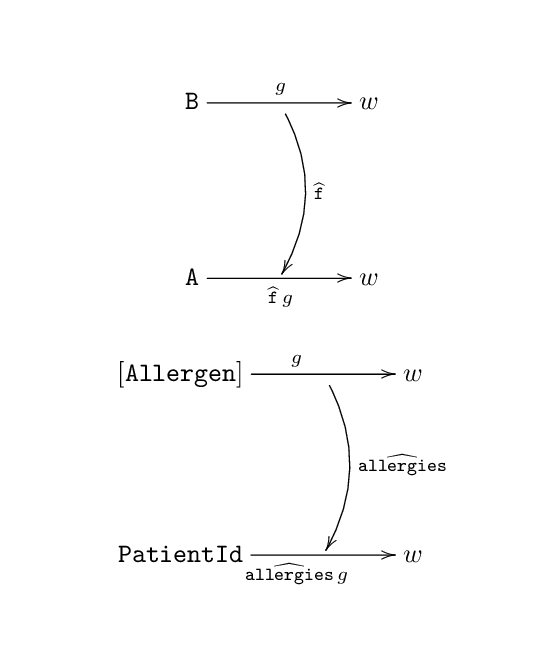
Figure 5: the action of the hat-transformed allergies function on an arbitrary function g.
And this is the lesson. \( \widehat{\mathtt{f}} \) is a function that you use in order to modify the source type of other functions.
Specifically, hat f changes a function’s source type from B to A.
How does it do that?
If you think about it for a moment, there’s really only one way it can do that.
The only possible way hat f can work is if there is some pre-processing on the input A value.
In fact, it must necessarily feed that A value to f in order to get a B value that it can then feed to \( g \).
We remind ourselves, what was hat f?
It was (. f) all along.
But now we know that it has to be function composition, specifically preprocessing.
The signatures themselves lock this requirement into place.
There’s no other way to satisfy the signatures.
In summary, here’s how to think about (. f).
(. f) is a higher-order function that you use to convert a B-eating functions into an A-eating functions.
(. allergies) is a higher-order function that you use to convert a [Allergen]-eating function into a PatientId-eating function.
Epilogue: Case in Point
We’d like to have a function that tells us whether or not a patient is allergic to a particular allergen.
Specifically, we’d like a path from (Allergen, PatientId) to Bool.
Alternatively (and equivalently), we need a path from Allergen to PatientId -> Bool.
To each patient is associated the list of allergens harmful to them. Our task presupposes that this association is given.
allergies :: PatientId -> [Allergen]For any particular allergen, it’s a straightforward task to write a function that checks for the presence of that allergen in any given list of allergens. In fact, this is such a common, formulaic task that the standard library provides a function for generating such allergen-list-checking functions.
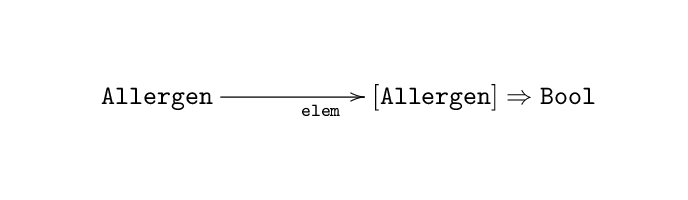
Figure 6: elem is a function that generates functions that eat lists of allergens
elem takes us from Allergen to [Allergen] -> Bool.
The last thing we need is a way to get from [Allergen] -> Bool to PatientId -> Bool.
In other words, we need a way of converting [Allergen]-eating functions into PatientId-eating functions.
Since allergen goes from PatientId to [Allergen], (. allergen) converts [Allergen]-eating functions into PatientId-eating functions.
Thus, (. allergen) takes us from [Allergen] -> Bool to PatientId -> Bool.
The function we’d like to have is the result of following the path from Allergen, along elem through [Allergen] -> Bool, then along (. allergies) to PatientId -> Bool.
Following a path of arrows represents the composition of the functions represented by those arrows.
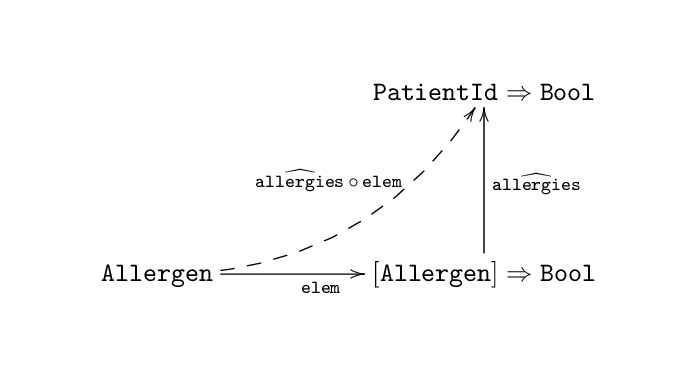
Figure 7: following the path along elem and the hat-transformed allergies function gives us the function we needed
Hence
isAllergicTo = (. allergies) . elem